Reductionism, a philosophy that seeks to handle complexity by breaking into parts, serves as the corner stone for industrial revolution and modern capitalism world. However, The whole is often greater than the sum of its parts, and the attempt to understand complex systems through reductionism neglects the interactions, emergent behaviors, and non-linear dynamics within the system.

In neuroscience and artificial intelligence, attempting to understand consciousness through the examination of individual neurons can't answer how consciousness emerge from those simple parts, as well as trying to create intelligence by connect neurons in a predefined way, whatsoever it's convolutional, hierarchical or recurrent. Similarly, In ecology, reducing an ecosystem to its individual species is unable to explain the stability,resilience and at the same time, the fragility of ecosystem.

Aside from those complex system, even simple deterministic system may show unpredictable behaviors. In this article, We focus on those systems described with simple mathematical formula and describes some theory to analysis them.

Define Chaos

For a particular mathematical formula or computation process(like calculate the trajectory of three body system, predict weather ,etc), a slightly different initial condition, or input, would result in very different result.

What does this sensitivity implies? For an computation process to be useful, we usually expect to get similar result for similar input, otherwise the output is not meaningful since a small rounding error will invalidate the result.

sensitivity to initial condition

To display the essence of chaotic behavior, we start from simple deterministic mathematics formulas.

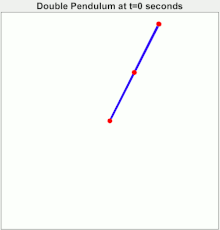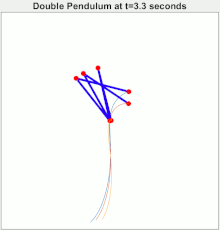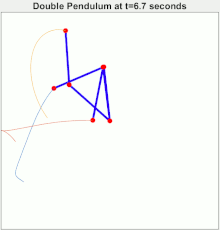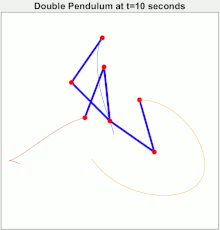
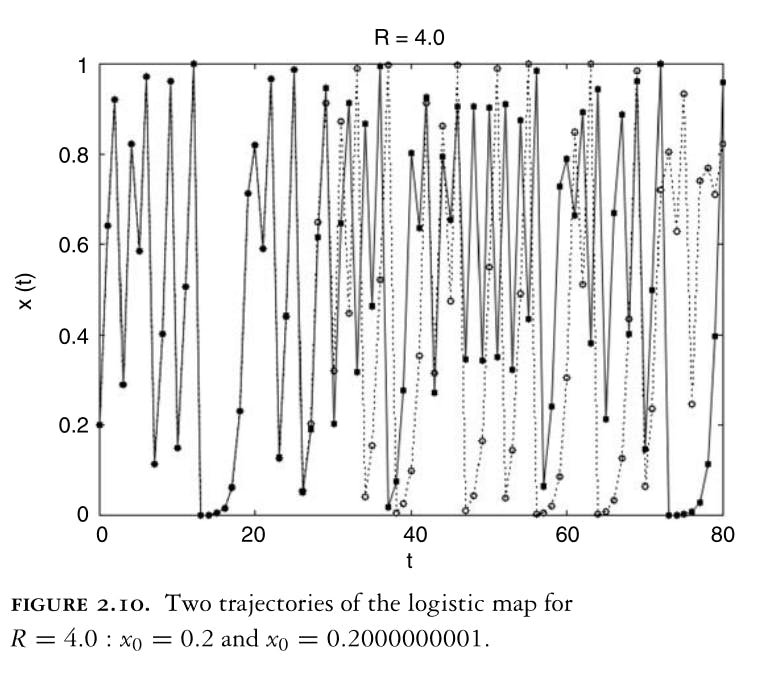
Example: a slightly different initial condition would result in a vastly different trajectory

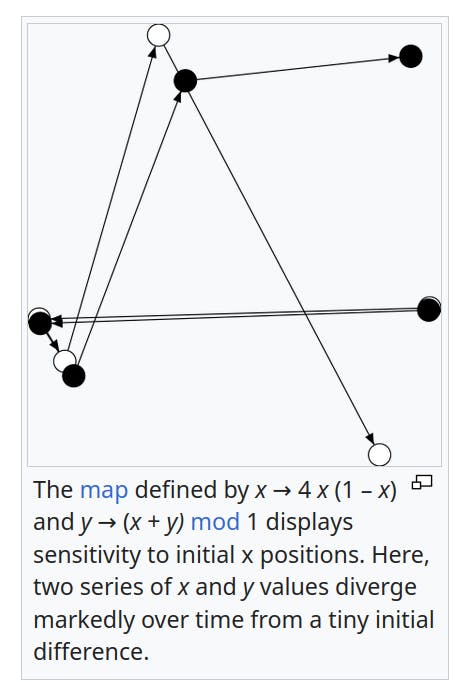
Example: Three 2 node system with slightly different initial condition:

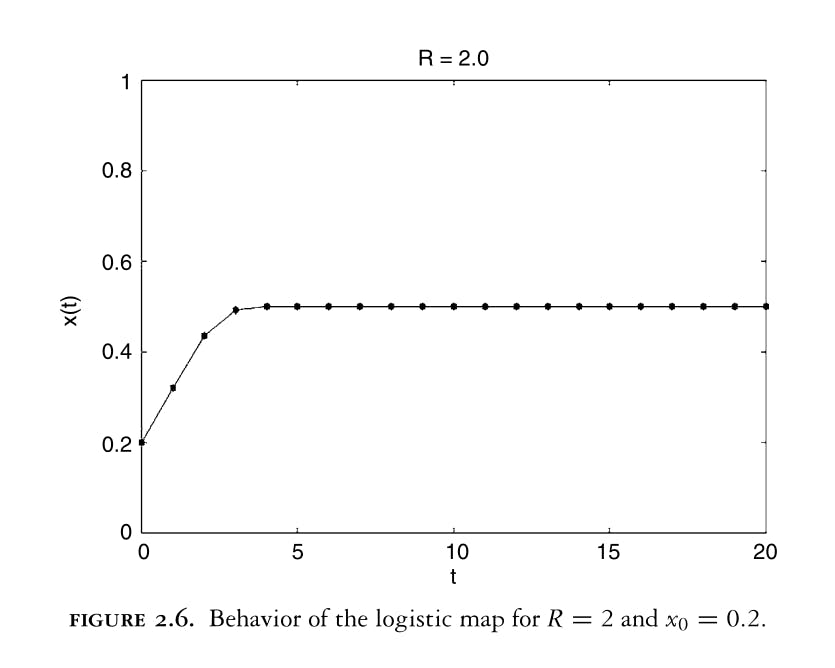
Example: logistic map

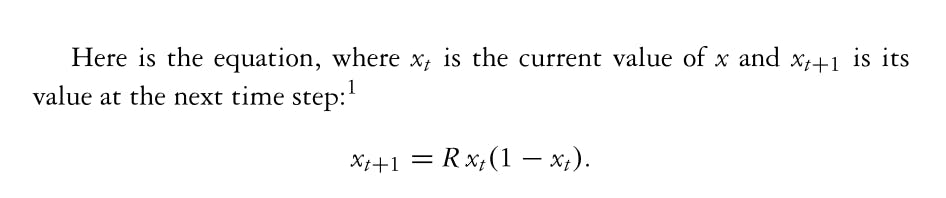
Example: Three-body problem

Example: Biosphere II was a expensive failure to create a self-sustaining replica of Earth ecosystems.

Describe and analyze Chaos: dynamical systems theory

Although we can't calculate chaotic system in the usual way, there are some new tools that will shed some light.

bifurcation diagram

for the logistic map example we just discussed, this diagram plots the stabilized x value versus the parameter R:

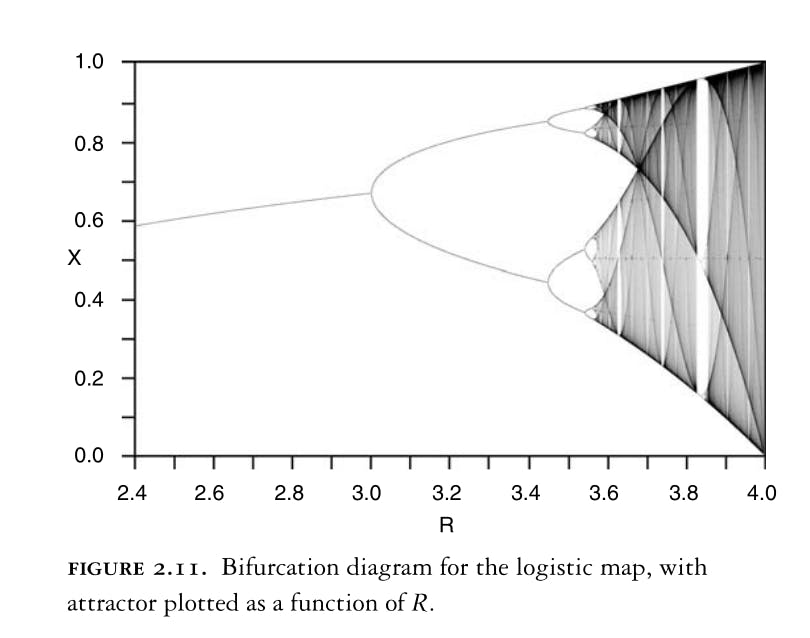
As the parameter R increase at 3.0, X have more possible values.

phase space

In dynamical systems theory and control theory, a phase space or state space is a space to display all possible "states"(positions), in contrast to the trajectory(position at specific time t) of the system.

Example: https://verzep.github.io/Learning-Lorenz/

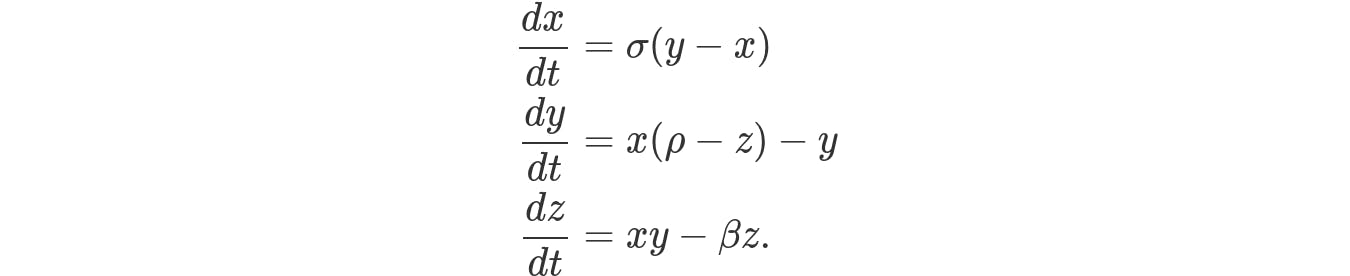
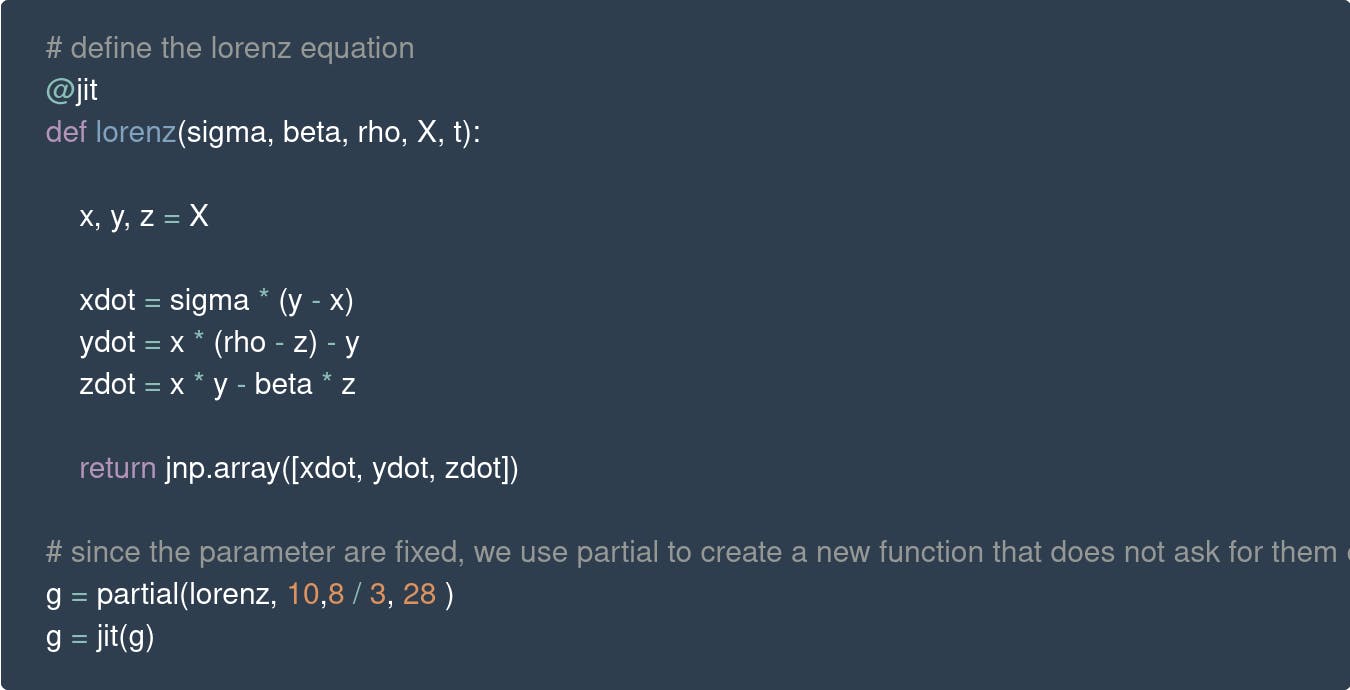
In space (x,y,z) - time

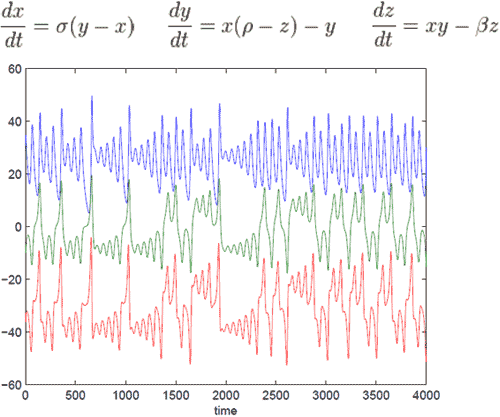
In phase space (x,y,z):

Feigenbaum constant:

The constant represents the ratio of the difference in parameter values at which successive bifurcations occur as a system undergoes a period-doubling route to chaos. It has an approximate value of 4.6692.

TBD

Renormalization

TBD

AI and the failed prediction of Chaos

TBD
Lorenz System https://verzep.github.io/Learning-Lorenz/

Reference:

https://en.wikipedia.org/wiki/Three-body_problem

Complexity: A Guided Tour , by Melanie Mitchell

https://en.wikipedia.org/wiki/Chaos_theory

lorenz equation: https://www.math.fsu.edu/~bertram/lectures/Chaos.pdf

https://verzep.github.io/Learning-Lorenz/

https://gereshes.com/2018/11/19/chaos-and-the-double-pendulum/

QA:

I presented this in a meeting and got some good questions:

Are chaotic systems calculable?

yes, if you have extremely accuracy of the initial condition. There're two way to address this: 1. we continue to quest for higher precision. 2. we accept this difficulty and give up for precise prediction/computation

In addition, someone mentioned Kolmogorov–Arnold–Moser about the persistence of quasiperiodic motions under small perturbations, which can be seen as a special case when computation is desirable.